enginedopa.blogg.se - Special right triangles side lengths

īased on this information, if a problem says that we have a right triangle and we’re told that one of the angles is 30º, we can use the first property listed to know that the other angle will be 60º.

In right triangles, the Pythagorean theorem explains the relationship between the legs and the hypotenuse: the sum of the length of each leg squared equals the length of the hypotenuse squared, or \(a^2+b^2=c^2\).

In right triangles, the side opposite the 90º angle is called the hypotenuse, and the other two sides are the legs.In addition, here are a few triangle properties that are specific to right triangles:

This means that all 30-60-90 triangles are similar, and we can use this information to solve problems using the similarity. Triangles with the same degree measures are similar and their sides will be in the same ratio to each other.You can see how that applies with to the 30-60-90 triangle above. In any triangle, the side opposite the smallest angle is always the shortest, while the side opposite the largest angle is always the longest.In other words, if you know the measure of two of the angles, you can find the measure of the third by subtracting the measure of the two angles from 180. In any triangle, the angle measures add up to 180º.Here are a few triangle properties to be aware of: How do we know that the side lengths of the 30-60-90 triangle are always in the ratio \(1:\sqrt3:2\) ? While we can use a geometric proof, it’s probably more helpful to review triangle properties, since knowing these properties will help you with other geometry and trigonometry problems. If you recognize the relationship between angles and sides, you won’t have to use triangle properties like the Pythagorean theorem. On standardized tests, this can save you time when solving problems. Knowing this ratio can easily help you identify missing information about a triangle without doing more involved math. Here is an example of a basic 30-60-90 triangle:

The side opposite the 90 º angle has the longest length and is equal to \(2x\).

The side opposite the 60º angle has a length equal to \(x\sqrt3\).

The side opposite the 30º angle is the shortest and the length of it is usually labeled as \(x\).

Because the angles are always in that ratio, the sides are also always in the same ratio to each other. Here’s what you need to know about 30-60-90 triangle.Ī 30-60-90 triangle is a right triangle with angle measures of 30 º, 60º, and 90º (the right angle). Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the no-calculator portion of the SAT. With special right triangles with angles of 45 45 90, this same formula can be applied.The 30-60-90 triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT. With the hypotenuse, we have information to determine the following: If you wanted to take a look at more examples of the 45 45 90 triangle, take a look at this interactive online reference for this special right triangle. You also happen to know a nice formula to figure out what the length of the hypotenuse is (the Pythagorean Theorem) and we'll show you how it will be used.

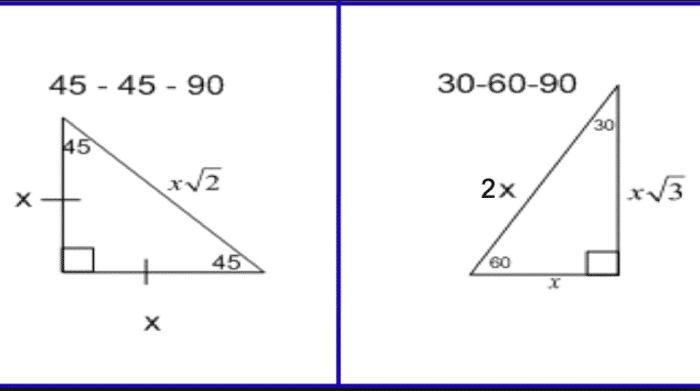
Since you'll also find that this triangle is a right-angled triangle, we know that the third side that is not equal with the others is the hypotenuse. It is an isosceles triangle, with two equal sides. One of these triangles is the 45 45 90 triangle. For a list of all the different special triangles you will encounter in math. These are the ones you'll most typically use in math problems as well. But for the ones that do, you will have to memorize their angles' values in tests and exams. There's not a lot of angles that give clean and neat trigonometric values. Special triangles take those long numbers that require rounding and come up with exact ratio answers for them. When numbers are rounded, it means that your answer isn't exact, and that's something that mathematicians do not like. Most trig questions you've done up till now have required that you round answers in the end. Special triangles are a way to get exact values for trigonometric equations.